New Energy of Conservation. Negative Space? Notes about the reversibility and heat transfer.
It takes the world to learn and to teach math, we could not reach our contemporary math progress without the ancient mathematicians from around mathematic community.
Dr Einstein was not born in America, but he helped Uncle Sam to build the world first atomic bomb, to necessarily win the World War II and to kill the civilian customers in Japan.
Except the atomic bombs, those were the immagine powers, kind of power people could live without for more alive customers from both sides.
The economists are believing that any firm in the world should plan in first priority for the best education possible. However, many intelligent agencies in the world wanted to learn but not to teach the advance math, they have one thing in common when we compare to the successful private companies: Spending billions and billions of dollars for the new products to be known. So you are the lucky one, you do not have to pay more money for R&D to generally know a portion of my works in the rare math.
I registered 4 copyrights in the rare math as citing below: Please check below copyright numbers to access my works at U.S. Library of Congress, or wait to see my software named LCDatabase and a booklet for:
TXU 234 996:
Multiplication & Division Integrations, March 11, 1986. To continue your solutions, which are not shown in Mathematical Hanbook.
TXI 1 944 003:
Program PVT Process, July 29, 1986. Beside Boyle's Law with constant Temperature, as Charles and Gay-Lussacs' Law with constant Pressure, here come two new rules with constant Volume in the fall and raise of Pressure and Temperature. Fortran language, disk is not available.
TXU 538 188:

Labor Expansion Program, September 9, 1992. Old GW-Basics language. This software has the new spreadsheet style which will give you the optimum choice between many known parameters, such as computing the profit based on the new workers to be hired. The weekly work hours will be reduced for the same work load after the new hires. When the profit and tax money are raised from increasing productions everywhere, a portion of new profit will reimburse the tax deduction for government, or pay off a loan for the bank, to balance the new benefit cost from the new hires. My brief description about the job creations was shown on Facebook by Can Le and Raise Tax.
TXU 794 158:
4-Works, Jan 02, 1997. Registered by Return Receipt number EG640110368 on DEC 1994. Including Graphic, Math, Word processor, and a Checkmath Checkbook program to detect the numerical errors by machines as well as operators.
TXU 242 815: The Accurate PI, June 16, 1986. To compute the variable PI number from various radii for the extreme precisions:
PI=2.16E-12/(R*Asin(1.2E-14/R))
Please noting that your popular PI=3.141592654 from books, calculators, and computers is setting at the value without R or R=1. The above exponent constant number was rounded up as Carbon 12-14 in Oxide Carbond is found on most surfaces.
THE PROOF OF THE VARIABLE Pi:
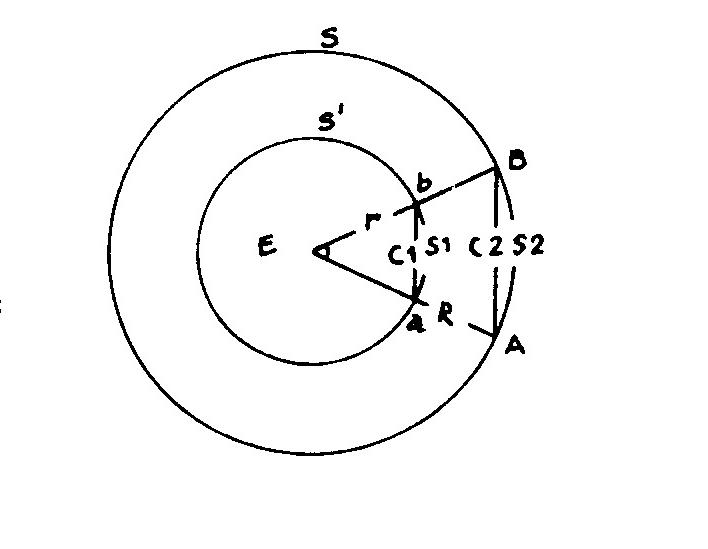
Given:
Two circles E(r, S1) and E(R, S2).Proving that PI1 <> PI2 (<>: Not equal)
Two similar triangles aEb and AEB give:
ab/r = AB/R , or:
C1/r = C2/R . We denoted equation (1)
From circumference S and diameter D:
Pi = S/D = S/(2R)
S = n(S2) and S' = n(S1)
c = Shortest chord.
s = Shortest curve.
c = s.
n = Numbers of equilateral curve s or chord c.
E = Epsilon degree angle.
By multiplying (n/2) into equation (1) above, we have:
(n/2)(C1/r) = n(C1)/(2r) = S'/d = PI1 = n(C2)/(2R) = S/D = PI2
The old formula which set PI1 = PI2 is true if and only if C1 <> C2 .
However, for the accuracy of PI, we should have variables n and S:
- The great n= S/c for any radius.
- The shortest chord c or curve s must be an infinitesimal number and constant for all radius us of certain surface, about 2 angstroms for both .
A constant numerator c or s divides by a variabIe denominator of radius r or R will yield a variable quotient.
For C1 = C2 = c and r <> R. Multiply c to both sides of this equation:
C1/r <> C2/R , then multiply 1/2 to both sides for:
n(C1)/(2r) <> n(C2)/(2R)
S'/d <> S/D
PI1 <> PI2.
The PI number is not the same for all radii at the nth equilateral sides from one constant chord c, different circumferences S .
If you did not satisfy the answer for the variable PI from above math, here is another proof:
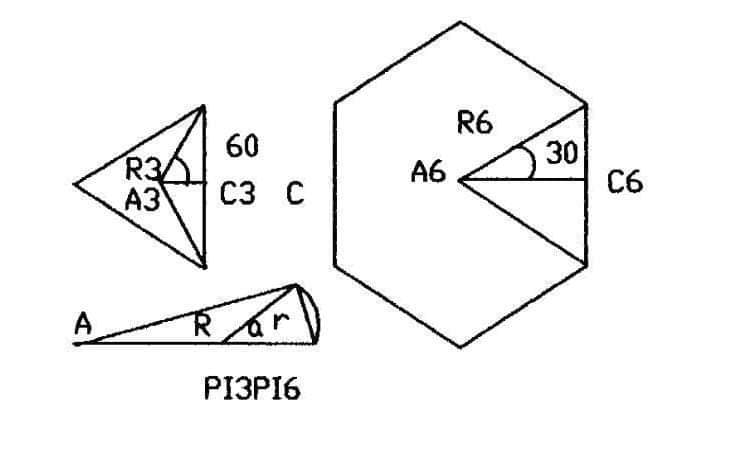
We are considering the smallest coarse circle as a triangle with equilateral sides C3, as it is inscribed in a circle radius R3, center angle A3, perimeter P3, the circles are not shown in Figure PI3PI6:
We have from side C3:
(C3)/2 = R3* sin (360°/(2*3))
(C3)/2 = R3*sin 60° .
For perimeter of an equilateral triangle:
3*(C2)/2 = 3*R3* sin 60°
3*(C2)/(2*R3) = 3 * sin 60° . We denoted equation (1).
PI3 for Triangled coarse circle:
PI3 = 3*(C3)/(2*R3) = 3 * sin 60° =3*( 0. 866) = 2.598
PI3 =3*(C3)/(2*R3) = 2.598 . Equation (2)
Similarity for a regular polygon of an hexagon, which is a coarse circle Radius R6, center A6, side C6, and perimeter P6:
6*(C6)/(2*R6) = 6 * sin (360°/(2*6)) = 6 * sin 30° . Equation (3).
We have by definition, PI6 for hexagonal coarse circle:
PI6 = 6*(C6)/(2*R6) = 6 * sin 30° = 6 * (0.5) = 3.0
PI6 = 6 * (C6)/(2*R6) = 3.0 . Equation (4).
By definition of PI = Perimeter / Diameter, and 2 equations (1) and (3):
We are considering constant side C3 = C6 for a shortest obtainable side, or curve and chord C as a common side, at different perimeters P3 and P6, which is equal to 1 diameter of 2 gold atomic radii at R = 1.46 angstroms:
From equations (2) and (4):
PI3 =3*(C3)/(2*R3) = 2.598
C3 = 2.598 * (2*R3)/3 . Equation (5)
PI6 = 6 * (C6)/(2*R6) = 3.
C6 = 3* (2*R6)/6 = R6. Equation (6)
For C3 = C6: 2.598*(2*R3)/3 = R6
R6/R3 = (2.598/3)*2 = 1.732 . Equation (7)
(1): 3*(C3)/(2*R3) = 2.598 . Same as ( P3 /D3)
(3): 6 * (C6)/(2*R6) = 3.0 . Same as ( P6/D6)
3*(C3)=(2*R3)*2.598 = P3 . Equation (8)
6*(C6)=(2*R6)*3 = P6 . Equation (9)
As we could examine the ratio by number of equilateral sides from (6/3):
(8) and (9): P6/P3 = 6*R6/(5.196*R3) = (6/5.196)*(R6/R3)
P6/P3 = 1.1547 *(R6/R3) . From (7):
P6/P3 = 1.15473441108545*(R6/R3)= 1.15473441198545*1.732
P6/P3 = 2.0
R6/R3= 1.732
From (1) and (3), we have the general formula to compute perimeter Pn for PIn from a large circle, or equivalent polygon with n sides, unit side or chord Cn, angle An; radius Rn:
Pn = 2 * Rn * sin (360/(2*n))
Pn = 2 * Rn * sin (180°/n) where A°n = (180°/n)
These results also shown that when the radius of a circle is larger in 1.732 times, then the perimeter of the larger circle (hexagon) is larger in double than the smaller coarse circle, for any standard side or chord C3 = C6. The more number of sides C we have the smoother circle it becomes at different PI. Please distinguish the variable n and angle A° with its constant equilateral side C, for different circles.
If PI is a constant, then the ratio R6/R3 should also equal to 2 ?
PI3 = 2.598 is not the same as PI6 = 3.0 . So it is fair to say that Pi number is not a constant number.
Since sin 1° = 0.017452406 is not proportionally and decimally increase with sin 10° = 0.173648177, and when r is greater to R, sin (180°/ A°) is also raised from at least 3 sides to n equilateral sides, at millions, for a larger circle from one unit chord C, for different PI numbers.
References:
1. PI pages: http://www.cecm.sfu.ca/pi/pi.html
2. Definitions of points: http://mathworld.wolfram.com/Point.html
3. Atomic radius:
http://www.chemguide.co.uk/atoms/properties/atradius.html: How did they measure atomic radius: "The atomic radius is defined as half the distance between the centers of neighboring atoms".
Trisect Angle Problem of Archimedes (287-212 B.C.) and Napoleon's quest:
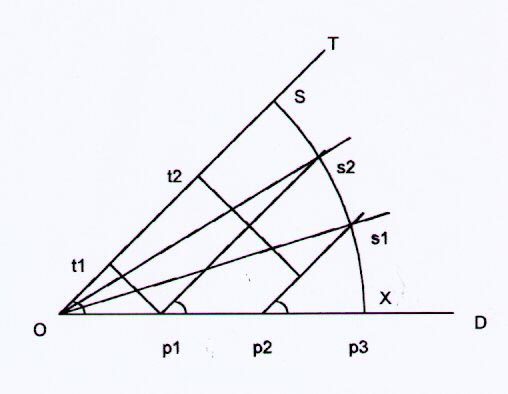
When I was at the tenth grade in high school, my math teacher told us a rare math problem, which no body could solve: How to divide an angle O into 3 equal smaller angles (trisection) by a compass and a ruler? Here was my trick from high school:
From 1 side D of angle O, we draw 2 parallel lines to another side T at 3 equal segments p1, p2, and p3 which start from O to a lenght X, with the proportion: (3/3)Op3=(3/2)p1p3=(3)p2p3; then an arc S-p3 having center O and radius Op3, wherein two parallel lines above divide arc S-p3 into 3 equal arcs from the same proportion above:
(3/3)Sp3=(3/2)s2p3=(3)s1p3.
From 3 equal segments Op1, p1p2, and p2p3, with 3 equal angles O, p1, and p2; we have p1 and p2 reach O at the same time when s2 and s1 reach S, for 3 equal sectors or 3 equal triplets from angle O.
In the computer language selection, the older the compiler you have, the less interference you encounter, unless you wanted the new versions with more complexities and features. The other computer got to have your DOS 4.0 or 5.0 with Gw-basic compiler to be able to read your file. Microsoft refused to license Gw-basics compiler to me for distribute my applications. When there is time for a needing large compiler, the new version will be released for your convenience with the reasonable and fair prices.
The above copyrights were selectively sent to: The International Mathematical Journal, National Academy of Sciences, National Science Foundation, University of Texas at Arlington, University of Dallas, and the White House.
In addition to the cited distance -x from Inertia -a=F/m (1), specific gravity g=m*m'/x (2), and uniform electric field E=F/q (3). By replace m from (2) into (1): F/-a = g*x/m' (4), then plugging F in (3) into this new equation (4) to have distance:
x=-E*q*m'/(a*g)
Substitute acceleration a=v/t, from velocity v and time t, we have Unify formula: x=-E*q*t*m'/(v*g)
Where the units are: Acceleration a=M/s² (meter/second²), force F=N newton, mass m or m'=Kg (m' standing for derivative m, as m1 or m2 also), distance x=M, electric field E=N/C coulomb, charge q=C, and specific gravity G=Kg.s²/M². According to the text books from College Physics, with Robert Resnick, David Halliday, Frederick J. Bueche, and many others, the Law of Universal Gravitation provided the gravitaional attraction force F=G*m1*m2/r², where the Cavendish experiment being accepted for universal gravity G=6.672E-11 N.M²/Kg², for which we have: r²=-F*G*m2/(a*E*q) m². The negatie sign of x or r² has a positive absolute value, which are reduced by the attraction force of gravity.
If Cavendish obtained the universal gravity G with the total lines of forces N per cross-sectional area of a sphere, or the arc and period of the rotating masses, which included the constant PI number, there is a little error in these calculations, since we have PI number being a variable which change with its radii. The resistance from space between 2 masses is counted in the permittivity and permeability constants of the electric field E, assuming Cavendish's G number was accurate in a moving earth within the speeding galaxies, and without the interfence from ESD.
Wherever the gravity is diminished, the distance -x will extend to the outer limit, equation (2) above shown 2 masses m and m', if m is 0 at the begining of only 1 pure great chrystal mass m' existed, as mass m is canceled in computing the distance x. The original universe of independent mass m' could not form a compound for the explosion of Big Bang to take place?
The whole imperfect Newton Laws remaining true with the First Law: A body at rest will remain at rest.
I posted in PhysLink on Nov-22-99 at 04:13aAM (EST). Rewritten by Nov-29 to 12-15-1999.
The classical physics said: The energy can only be transformed, not created nor be destroyed.
If you drop the same weight 10N (W1=1 and g=9.81) from the same height, h=1 meter, onto two point of applications or two ends of a 3 meters long fulcrum which is horizontally stayed still on a pivot by 2 different nails W2 and W3, both nails have equal lenght and are secured to stand on fulcrum by the same distance from pivot, r=0.1 meter each; thereby, one end l of fulcrum is 1 meter from pivot, while another end L is 2 meters, and the heavier nail W2 is located on the shorter side l of fulcrum, on the left, for horizontal balance.
l ____W2_^_W3________ L
What is the energy transformed from one end of the fulcrum to another end at each nail?
The same Potential Energy (P.E.) from one height h will transform into the Translational Kinetic Energy (T.K.E.) plus the Rotational Kinetic Energy (R.K.E.=I*w²/2); the Moment of Inertia I (Torque/Agular Acceleration), and w is Angular Velocity of the nail on the arm of fulcrum after time t. The mass correlations of 2 nails and 2 arms of fulcrum are balanced, or canceled out, while the Newton's Third Law gave the reactive force then torque. Start at the shorter arm of fulcrum, we have:
The turning effect, or Torque = Force * Distance = W1*g*l
The Second Condition for Equilibrium, or Newton's Third Law: W1*g*l=W3*g*r or W3=W1*l/r
Substitute the values for a balanced mass W3=W1*(1/0.1) or new resultant W3=10*W1
T.K.E=W3*v²/2 = (10*W1)*v²/2
If W3 has its initial velocity v0=v=g*t as it just transformed and redirected after time t=1 or less second, in the opposite direction, whereby the acceleration or deceleration is not a constant; gravity g is vertically diminishing to a zero value at maximum height, and v=-g*t when we compute R.K.E. after time t1; from a limited W1 and the minimized W3:
P.E.=W1*g*h=1*9.81*1 for about 10N We usually have had v=(2*g*h)½ for a slided or rolled object at the same mass, after the impact; however, without the balanced fulcrum and at the different masses, we have v=(W1*g*h/W3)½. From the instantaneous initial velocity :
T.K.E.=W3*v²/2 = (10*1 Kg)*(9.81*1 sec)²/2 T.K.E.=500 J from 10 J of P.E.
From the earlier subject, we have had g=m*m'/x, the weight of W3 increased with g as x is smaller toward the axis of pivot point or center of the earth; the lower altitude has more earth magnetic or gravity field, and therefore the mass W3 should also be increased. The gravity field works as the earth magnet which attracts the radiated objects by the gliding action as the rain water falls into the exit line of a gutter; or when you simpby catch a butterfly by a deep spoon net wherin the net is similar to the gravity field or rays; since any substance above the absolute zero degree always emits radiations. This gravity g can be replaced by acceleration a or inertia i wherever g is approaching zero value.
Without the friction and the negative sign of reactive torque is ignored from the increased value of torque; if you chose -g in P.E. then v=+g*t, as the counterclockwise torque is positive while the clockwise torque is in minus sign; we have more than 10 times the instantaneous Translational Kinetic Energy at the lighter and faster nail, on the right, from the greater w (w=v/r) at a shorter distance r.
The same principle is applied to the longer arm on the right, for the torque at W2=W1*L/r or W2=20*W1; since the resultant forces at W2 or W3 are in equilibrium, if W2 and W3 are driven by the same and only K.E., the initial instantaneous velocity of W2 and W3 should be equal, but we known that both have the different torques from the induced various masses; for greater energy at W2.
Why the weight W2 became more greater than W3 on the longer arm L, not as equation g=m*m'/x only claimed for mass W3 above? We have a smaller ratio from W2:
(r/L)<(r/l) over the point of pivot, while ratio over center of earth radius R: Angular distance =w*t=X/R where X is distance of W2 and arm L. Angular frequency w=2*PI*f
(Frequency f of oscillation, for ray from L to W2 in horizontal motion as a spring, if you agree that weath can not become bread without been heated up by rays!)
X/R=2*PI*f*t=(r+L)/R
f=(l+L)/(2*R*PI*t). We have longer L for greater f and mass? 1/(w*t)=1/=R/X.
The period T=1/f=2*PI*(L/g)½ of a similar width=8>=R/X.
The period T=1/f=2*PI*(L/g)½ of a similar half cycled pendulum at a simple harmonic motion with small angle, longer L for greater mass, and smaller f for a larger T, then faster v at the other end l with the same r but much shorter in ratio. In addition from P.E. which has the effect from gravity g and altitude h, and the momentum induced it, the momentum is a product of mass and its velocity, for the fulcrum to change it.
The Rotational Kinetic Energy is ignored for a moment, and we have the different impact works. The various torques "created" the different energies on earth? This is not a nuclear energy but another application of the Momentum Energy from the changes of: Distances, altitude, and velocities about the point of pivot or center of gravity.
Moreover, if the same light being exposed on the same solar cell panel, or the same weather could create the different static electricity on the same object at the changing locations of the same address, which are depended on gravity, altitudes, and velocities from the rotating earth and our expanding universe?
Fusion:
Nuclei reactions by cohesion force which fuse or melt together then release the fusion energy.
The reactions simultaneously get and give a large amount of heat from conventional devices such as the typical radiography beams and other lasers, beside the related fields are piezoelectric and ESD devices.
The author reserved the future publications of his copyrighted materials.
You can use PI formula and the document for school works with the reference of the author name, but do not reproduce these for your commercial products or book without written permission from author.
From Heatransfer text book: Any substance at temperature above absolute zero degree will emit radiations. A colder substance than zero degree may not radiate, so the body having the higher temperature emited radiation to the colder body.
For any temperature other than absolute degree, the higher or lower temperature will emit more or less radiations which is based on temperature gradient, area of heat conduction, and thermal conductivity.
If temperature of the colder body is transferred to the hotter meal by discharge the heat to the hot meal, then the larger stomach will lower the temperature to freeze the meal.
To beat the old laws you have to beat Fourier's law of heat conduction q with experiments:
q= -k*A*(δT/δx)
The minus sign for Second law of Thermodynamics, thermal conductivity constant k, area A, and temperature gradient (delta T/delta x), temperature gradient is the change in temperature and distance of heat conduction.
Example for a cup of hot tea we have q<0 while a cup of ice will have q>0 for gaining heat, when both cups are cool to room temperature by heat conduction.
When heating the colder liquid, it will take longer time to reach the boiling point than the warmer liquid.
Since cold temperature alone will not create energy but the heat does, and it takes energy or heat to boil a cold liquid by adding heat to it. If heat was taking off from the colder liquid to transfer to the hotter liquid by other than 3 normal ways: Conduction, convection and radiation, the hot liquid will remain hot.
The greater temperature gradient delta T, the hotter liquid, and the faster you lose energy q from emitting radiations, beside the greater k and A, and smaller distance delta x.
It is not the colder body that transfers heat to the hotter body, but the radiation from the hotter body within the thermal gradient which do the work or heat transfer.
Contribution in Science and Technology.
Click on photo (will add to this page) for detail view.
Can Le